책 '데이터 중심 애플리케이션 설계' - 3장. 저장소와 검색을 읽고 정리한 글입니다.
#️⃣ 1. 인덱스(색인)
1-1. 정의
- 데이터베이스에서 특정 키의 값을 효율적으로 찾기 위한 데이터 구조
- 어떤 부가적인 메타 데이터를 유지하는 것으로, 이정표 역할을 해서 데이터 위치 찾는데 도움을 줌
- 기본 데이터에서 파생된 추가적인 구조
- 쉽게 말해 책의 목차
- 대부분 데이터베이스는 색인 추가와 삭제 허용
- 색인은 데이터베이스 내용에는 영향을 주지 않지만, 질의 성능(읽기 속도 향상)에만 영향줌
- 특정 테이블의 컬럼 검색 시, 테이블의 레코드를 full scan하는 것보다, index화되어 있는 index 파일을 검색하여 질의 성능 향상 시킴
- 특히 쓰기 과정에서 오버헤드 발생함
- 이는 저장소의 ‘트레이드 오프’ ⇒ 색인 잘 선택하면 읽기 질의 속도 향상되지만, 모든 색인은 쓰기 속도를 떨어뜨림
#️⃣ 2. 색인(Index)의 데이터 구조
책에서는 키-값 색인 구조형태를 중점적으로 설명한다.
사전 지식. 로그(Log)
데이터베이스에서 append-only 데이터 파일
3-1. 해시 색인 (Hash Index)
✅ 이론
- 로그 파일의 간단한 색인 전략은 키를 데이터 파일의 바이트 오프셋에 매핑하여 인메모리 해시 맵을 유지하는 것이다.
- 만약 위의 형태로 로그 파일에 계속해서 추가하면 디스크 공간 부족 문제가 생길 수 있다. 이를 위해 로그를 특정 크기의 세그먼트(Segment)로 나눈다.
- 세그먼트 파일은 특정 크기에 도달하면 닫히고, 그 이후에는 쓰기를 새로운 세그먼트 파일에 수행한다.
- 세그먼트는 추가전용(append-only)과 불변(immutable)한 특성을 가진다.
- ⇒ 즉, 인메모리 해시맵과 디스크 상의 데이터 구조 세그먼트로 구성됨.


- 세그먼트 파일들은 컴팩션(compaction)을 통해 중복된 키를 제거하고 최신 갱신값만 유지할 수 있다.
- 보통 컴팩션 진행 시 세그먼트를 더 작게 만들어서, 조회 속도를 높일 수있다.
✅ 컴팩션(Compaction) 과정
- 세그먼트가 특정 크기에 도달하면 세그먼트 파일 닫고, 병합할 세그먼트는 새로운 파일로 만듦
- 고정된 세그먼트와 컴팩션 진행 (백그라운드 스레드에서 수행)
+ 컴팩션 수행 중에도 이전 세그먼트에서 읽기&쓰기 요청 처리 가능 - 병합 끝나면 새로 병합한 세그먼트로 전환
- 이전의 세그먼트 파일 삭제
✅ 장점
- 추가와 세그먼트 병합은 순차적인 쓰기 작업이라 무작위 쓰기보다 훨씬 빠른 편이다.
- 세그먼트 파일 특성 상 추가 전용&불변이므로 동시성과 고장 복구는 훨씬 간단하다.
- 오래된 세그먼트 병합은 시간이 지남에 따라 조각화되는 데이터 파일 문제 피할 수 있음
✅ 한계점
- 해시 테이블이 메모리에 저장되어 키가 많으면 문제됨
- 해시 테이블은 범위질의(range query)에 비효율적임.
특정 값 사이 모든 키를 스캔 불가하며, 해시맵에서는 모든 개별 키를 조회해야 됨
3-2. SS테이블
✅ 이론
- SS테이블(Sorted String Table; 정렬된 문자열 테이블): 세그먼트 파일 형식에서 정렬된 키-값 쌍을 가진 테이블 형태의 데이터 구조.
- 여러 SS테이블 세그먼트를 병합하고 각 키의 최신 값만 유지하여, 새로 만든 세그먼트도 정렬된 키 형태를 유지한다. 만약 다중 세그먼트가 동일한 키를 보유한 경우, 가장 최근 세그먼트 값은 유지하고 오래된 값은 버린다.
- ⇒ 즉, 인메모리 희소색인(sparse index)와 디스크 상의 정렬된 세그먼트 파일 (SS테이블) 구성임

✅ 장점 : SS 테이블이 ‘해시 색인을 가진 로그 세그먼트’보다 좋은 이유
- 세그먼트 병합은 파일이 사용 가능한 메모리보다 크더라도 간단하고 효율적임. 병합정렬 알고리즘 방식과 유사하게 세그먼트 병합함
- 파일에서 특정 키를 찾기 위해 메모리에 모든 키의 색인 유지할 필요 없다. 일부 키에 대한 오프셋을 알려주는 인메모리 색인만 있어도 빠르게 스캔 가능
- 레코드들을 블록으로 그룹화하고 디스크에 쓰기전에 압축하여, 디스크 공간을 절약하고 압축으로 I/O 대역폭 사용을 줄인다.

✅ SS테이블에서 데이터를 키로 정렬하는 방법
요약 : 쓰기 작업은 인메모리인 멤테이블로 유지하다가, 멤테이블의 크기가 커지면 ss테이블 파일로 디스크에 저장한다.
- 쓰기 들어오면, 인메모리 균형트리(balanced tree; 혹은 멤테이블(memtable)) 데이터 구조에 추가함
- 멤테이블이 임계값(보통 수MB)보다 커지면 SS테이블 파일로 디스크에 기록한다. SS테이블을 디스크에 기록하는 동안, 쓰기는 새로운 맴테이블 인스턴스에 기록함
- 이때, 트리가 이미 정렬된 키-값 쌍이라 효율적으로 수행가능하며, 새로운 SS테이블 파일은 DB의 가장 최신 세그먼트가 된다.
- 읽기 요청 처리하려면, 메모리에 있는 멤테이블에서 키를 찾고 →디스크 상의 가장 최신 세그먼트에서 찾는다. (다음으로 두번째 오래된 세그먼트, 세번째 오래된 세그먼트, … 등에서 찾음) (백그라운드에서 수행됨)
3-3. LSM 트리(Log-Structed Merge-Tree)
✅ 이론
- 바로 위처럼 쓰기 작업은 인메모리의 멤테이블에 추가되고, 멤테이블이 일정 크기에 도달하면 SSTable(Immutable Sorted String Table)로 디스크에 저장되는 형태가 LSM 트리 구조(로그 구조화 병합 트리)이다.
- 여러 층의 SSTable이 디스크에 저장되고, 백그라운드에서 주기적으로 해당 SSTables을 병합함으로써 중복을 제거하고 읽기 성능을 최적화함.
- LSM 저장소 엔진 : 정렬된 파일 병합과 컴팩션 원리를 기반으로 한 저장소 엔진
- 레벨(Level): LSM 트리에서는 여러 레벨의 SSTable이 존재한다. 각 레벨은 크기가 다르며, 일반적으로 레벨 0부터 시작하여 높은 레벨로 갈수록 SSTable의 크기가 커진다.

✅ 성능 최적화
1. 블룸 필터 (Bloom Filter)
- 집합 내용을 근사한(approvimating) 메모리 효율적 데이터 구조
- 데이터베이스에서 존재하지 않는 키가 있을 때, 존재하지 않음을 알려주어 불필요한 디스크 읽기를 절약 가능하다.
2. 크기 계층(sized-tiered)과 레벨 컴팩션(leveled compaction) 전략
- 크기 계층(sized-tiered) 컴팩션: 상대적으로 좀 더 새롭고 작은 SS테이블을 상대적으로 오래되고 큰 SS테이블에 연이어 병합하는 방법
- 레벨(level) 컴팩션 : 키 범위를 더 작은 SS 테이블로 나누고, 오래된 데이터는 개별 “레벨”로 이동하기 때문에 컴팩션을 점진적으로 진행해 디스크 공간을 덜 사용한다.
- “키 범위를 더 작은 SS 테이블로 나눈다” : 작은 단위로 데이터를 관리하여 읽기&쓰기 성능 최적화함
- “오래된 데이터를 개별 레벨로 이동” : 즉, 오래된 데이터에 대한 압축 및 정리를 한다.
- “점진적인 진행” : 레벨 컴팩션은 데이터를 작은 단위로 나누어서 점진적으로 진행함
3-4. B트리
✅ 이론
- 1970년에 등장한 B-Tree는 가장 널리 사용되는 색인 구조이다.
- 키로 정렬된 키-값을 쌍을 유지하기 때문에, 키-값 검색과 범위 질의에 효율적이다.
- 전통적으로 고정크기(4KB 혹은 그 이상) 블록이나 페이지로 나누고, 한 번에 하나의 페이지에 읽기 또는 쓰기를 한다.
- 각 페이지는 주소나 위치를 이용해 식별할 수 있으며, 페이지는 여러 키와 하위 페이지 참조를 포함한다.
- 한 페이지는 B트리의 루트(root)로 지정되며, 색인에서 키를 찾을 시 루트에서 시작된다.
- 분기 계수(branching factor) : 한 페이지에서 하위 페이지를 참조하는 수 (그림에서 한 페이지에 존재하는 ref수)
- 실제 분기 계수는 저장공간 양에 의존적인데 보통 수백개에 달한다.

✅ 색인에서 키 탐색
- root 페이지에서 시작하여, 페이지의 여러키와 하위 페이지 참조를 통해 여러 페이지를 거친 후, 최종적으로는 찾으려는 키가 있는 페이지(리프 페이지 (leaf page))에 도달한다.
✅ 키 값 갱신 방법
아래 알고리즘은 트리가 계속 균형 유지하도록 함
n개 키를 가진 B트리 ⇒ O(log n)
- 키를 포함하고 있는 리프 페이지 검색
- 페이지의 값을 바꾼 다음 다음 페이지를 디스크에 다시 기록함 (페이지에 대한 모든 참조는 계속 유효함)
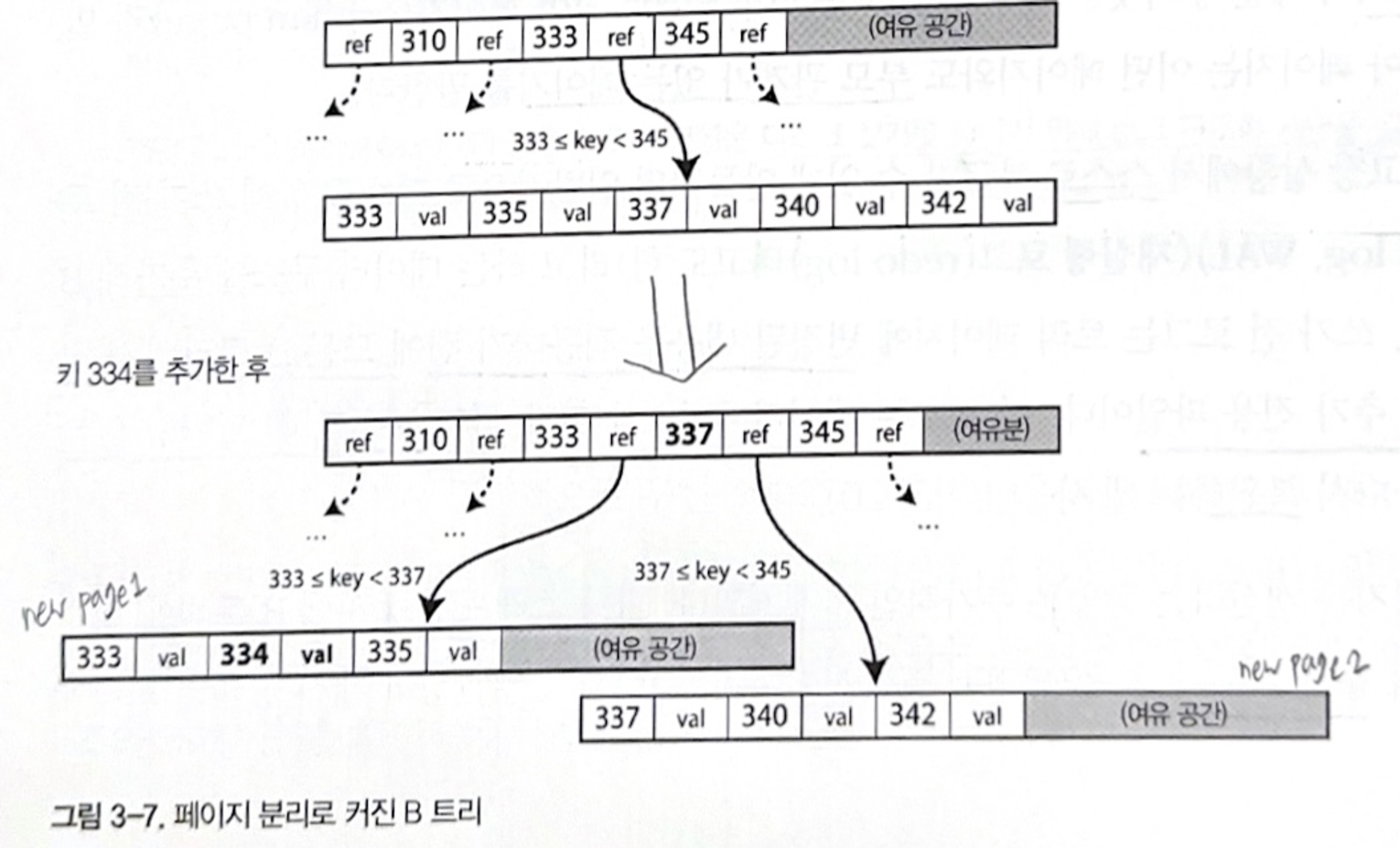
- 새로운 키를 추가하려면, 새로운 키를 포함하는 범위의 페이지를 찾아 해당 페이지에 키와 값을 추가한다.
- 만약 새로운 키를 추가할 페이지에 공간이 충분하지 않으면, 페이지 하나를 반쯤 채워진 페이지 둘로 나누고, 상위 페이지가 새로운 키 범위의 하위부분을 알 수 있게 갱신한다.
✅ 신뢰성 높이기 위한 B트리 부가 요소
- 쓰기 전 로그 (write-ahead log. WAL) (재실행 로그(redo log)
- B트리 기본적인 쓰기 동작은 새로운 데이터를 디스크 상의 페이지에 덮어쓴다. (LSM 트리와 대조되는 부분)
- 만약 여러 다양한 페이지 덮어쓰기를 하는 도중, 일부 페이지만 참조를 갱신하고 중간에 데이터베이스가 고장나면, 색인이 훼손되어, 고아페이지(orphan page; 어떤 페이지와도 부모 관계가 없는 페이지)가 발생할 수 있다.
- 이렇듯 데이터베이스가 고장난 상황에서도 스스로 복구할 수 있게 일반적으로 디스크 상에 WAL 데이터 구조를 추가하여 B트리를 구현한다.
- WAL는 트리 페이지에 변경된 내용을 적용하기 전에, 모든 B트리의 변경 사항을 기록하는 추가 전용 파일이다.
- WAL는 DB고장 시 일관성 있는 상태로 B트리 복원하는데 이용됨
- 래치 (latch)
- 같은 자리에 페이지 갱신과 같이, 다중 스레드가 동시에 B트리에 접근한다면 동시성 제어가 필요하다.
- 동시성 제어를 위해 래치로 트리의 데이터 구조를 보호한다.
3-5. B트리와 LSM 트리 비교
| LSM 트리 | B 트리 | |
| 읽기 속도 | 비교적 느림 • 이유 : 각 컴팩션 단계에 있는 여러 가지 데이터구조와 SS테이블 확인 필요 |
비교적 빠름 |
| 쓰기 속도 | 비교적 빠름 하지만 컴팩션 연산시 높은 쓰기 처리량 발생하여 많은 디스크 대역폭이 필요하다. |
비교적 느림 |
| 쓰기 성능 비용 (쓰기 증폭) |
B트리보다 쓰기 처리량 좋음. 쓰기 증폭 낮음 • 이유 : LSM 트리는 SS테이블의 반복된 컴팩션과 병합으로 여러 번 데이터를 다시쓴다. 하지만, 순차적으로 컴팩션된 SS테이블 파일 쓰기 때문에 비교적 쓰기 증폭이 낮다. |
비교적 쓰기 처리량 낮음. 쓰기 증폭 높음 • 이유1 : 트리는 기본적으로 모든 데이터 조각을 최소한 두 번(쓰기 전 로그와 트리페이지) 기록해야됨. 몇 바이트만 바뀌어도 전체 페이지 기록해야되는 오버헤드 존재 • 이유 2 : 트리에서 여러 페이지를 덮어씀 |
| 압축률 | 더 좋음. 비교적 디스크에 더 적은 파일 생성됨 • 이유 : 주기적으로 파편화를 없애기 위해 SS테이블을 다시 기록하므로 저장소 오버헤드 낮음 |
비교적 안 좋음 • 이유 : 파편화로 인해 사용하지 않는 디스크 공간 일부 남음 |
| 질의응답시간 | 예측 어려우며, 상위 백분위의 질의응답시간은 때때로 김 • 이유 : 디스크가 가진 자원은 한계가 있어, 디스크에서 컴팩션 연산이 끝날때 까지 대기시간 발생함. |
예측하기 쉬움 |
| 키 색인 위치 | 같은 키 다중 복사본 존재할 수 있음 | 각 키가 색인의 한 곳에만 정확히 존재함 그렇기에, 강력한 트랜잭션 시맨틱을 제공하는 DB에서 B트리가 더 좋음 |
| 최근 트랜드 | 새로운 데이터 저장소에서 로그 구조화 색인 점점 인기 얻고 있음 | 데이터베이스 아키텍처에 아주 깊게 뿌리내림 (사라질 가능성 적음) 많은 작업 부하에 대해 지속적으로 좋은 성능 제공 |
- 쓰기 증폭 (write amplication) : 데이터베이스에 쓰기 한 번이 데이터베이스 수명 동안 디스크에 여러번 쓰기를 야기하는 효과
- SSD는 수명이 다할 때 까지 블록 덮어쓰기 횟수가 제한되기 때문에 쓰기 증폭은 SSD에 중요한 요소이다.
- 쓰기가 많은 애플리케이션에서 성능 병목은 "DB가 디스크에 쓰는 속도"이다. 이 경우 쓰기 증폭이 바로 성능 비용이다.
출처
[책] 데이터 중심 애플리케이션 설계 - 3장
https://gyoogle.dev/blog/interview/데이터베이스.html
https://github.com/WooVictory/Ready-For-Tech-Interview/blob/master/Database/인덱스(INDEX).md
'#️⃣ CS (Computer Science) > Database' 카테고리의 다른 글
| 4장. 이진 부호화와 발전 (0) | 2024.02.02 |
|---|
